Кажется, без термина GTO сейчас не обходится ни одна дискуссия о покере. Это неудивительно, ведь оптимальные действия с точки зрения теории делают игрока абсолютно непобедимым. Как несложно понять из моего блога, я на 100% принадлежу к лагерю «оптималов», но у оптимального покера есть свои рамки, которые зачастую многими игнорируются, то ли в силу недостатка знаний, то ли из-за личного интереса. Понимание концепций GTO позволит любому игроку в покер (да, даже микролимитчикам) существенно улучшить свою игру, но это не Святой Грааль, решающий все проблемы и гарантирующий легкие деньги.
Важно понимать, что идеи GTO могут резко усилить вашу игру во многих специфических ситуациях. Однако за пределами игры один на один их нельзя использовать как основу для всей своей стратегии, полностью вытесняя стандартную игру. Ведь очевидно, что оптимальная стратегия для, скажем, 6-max игры в стеках 100 бб, на сегодняшний день неизвестна. Применение нашей программы (GTO Range Builder) тоже имеет немало ограничений. Это инструмент, позволяющий вам улучшить свою игру, а не решение покера.
Определение равновесия Нэша
Цитирую Википедию: «Так в теории игр называется тип решений игры двух и более игроков, в котором ни один участник не может увеличить выигрыш, изменив своё решение в одностороннем порядке, когда другие участники не меняют решения».
То есть человек, применяющий GTO-игру (или играющий согласно равновесию Нэша), гарантирует, что в случае, когда другие соперники также играют по Нэшу, ни один из них не может увеличить свое ожидание от игры, в одностороннем порядке изменив стратегию.
Сначала применим это определение к игре один на один, в которой GTO-покер действительно гарантирует непобедимость. А потом посмотрим на игру в 3-max, в которой начинаются трудности.
GTO в хэдз-апе
Предположим, мы играем хэдз-ап с рыбой и действуем идеально по GTO, в то время как рыба допускает много ошибок. То есть наш соперник отклоняется от GTO, а при этом он по определению не может улучшить свое ожидание. Так как покер – игра с нулевой суммой, а единственный соперник данного фиша – вы, то потерянное им математическое ожидание приобретается вами.
Если вы играете GTO, а ваш соперник – нет, то в хэдз-апе он никогда не сможет обыграть вас. Это сильное утверждение, и оно делает GTO-стратегии чрезвычайно привлекательными. Если бы оптимальная стратегия была известна (что, при отсутствии фундаментальных прорывов в развитии вычислительной техники, вряд ли произойдет в этом столетии для стандартного безлимитного холдема), это бы навсегда решило игру один на один.
За пределами HU
Сила GTO проявляется не только в том случае, когда карты на префлопе раздают двум игрокам. Ту же логику можно использовать для любых ситуаций, когда в игре остаются два человека. Если флоп смотрят двое, то с этого момента они играют хэдз-ап, и GTO-стратегия по-прежнему является непобедимой. Возможно, само ваше решение посмотреть флоп было ошибочным; оптимальная стратегия сможет точно определить максимальное EV данной ситуации, которое будет вам гарантировано вне зависимости от действий противника. Если противник будет играть неоптимально, ваше ожидание может только вырасти.
Подавляющее большинство покерных раздач к риверу играются один на один, поэтому применение стратегии GTO для хэдз-апа позволит вам резко повысить свой винрейт во множестве ситуаций, даже если вы играете 6-max или полный стол.
GTO в 3-max
Когда в игре три человека, привлекательность GTO несколько блекнет, так как снижение EV одного из наших соперников вовсе не обязательно ведет к возрастанию нашего EV. Довольно часто соперник, совершающий ошибки, тем самым понижает наш винрейт, даже если мы продолжаем играть оптимально. Простейший пример понять это – обратиться к пуш-фолд-игре трех человек в стеках 15 бб. Решение у этой игры достаточно простое:
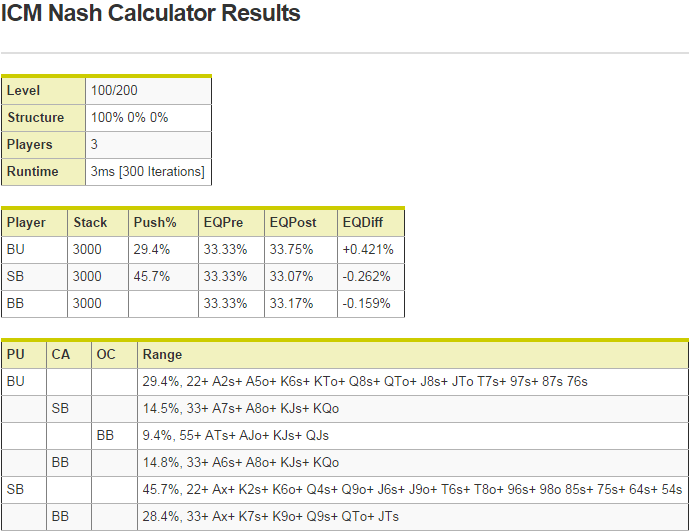
Баттон ставит олл-ин с 29% рук, малый блайнд коллирует с 14.5%, большой блайнд совершает оверколл с очень тайтовым диапазоном (9.4%), а после фолда от малого блайнда коллирует несколько шире (14.8%). Если баттон фолдит, малый блайнд пушит очень широко (46%), а большой блайнд коллирует на 28%.
Предположим, мы находимся на малом блайнде. Если ввести этот сценарий в аналитическую программу CardRunnersEV (я провел миллион симуляций по методу Монте-Карло; результаты, конечно, не отличаются абсолютной точностью, отчасти потому что CREV округляет винрейт до ближайшего целого числа), винрейты игроков получаются следующими:
Баттон: 19 bb / 100
(МЫ) Малый блайнд: -11 bb / 100
Большой блайнд: -8 bb / 100
Из определения равновесия Нэша нам известно, что игрок, отклоняющийся от оптимальной стратегии, понижает свое ожидание. Предположим, что баттон – вик-тайт, который пушит намного более узкий диапазон, чем требует покер. По определению это снизит его винрейт. Но Джон Нэш ничего не говорит о том, как это отразится именно на нашем ожидании!
Если баттон ставит олл-ин только с 55+, AJ+, KQ, KJs, QJs, JTs, ожидание игроков меняется следующим образом:
Баттон: 15 bb / 100
(МЫ) Малый блайнд: -17 bb / 100
Большой блайнд: 2 bb / 100
Наше ожидание падает на 6bb за 100 рук, несмотря на то, что мы по-прежнему играем по Нэшу. Оно падает сильнее, чем у игрока на баттоне, несмотря на то, что все эти изменения вызваны именно его ошибками! Если во всех прочих ситуациях игроки действуют по GTO, наш общий винрейт в этой игре становится отрицательным: выигрываем на баттоне 19 бб, проигрываем на малом блайнде 17 бб и играем большой блайнд в -8 бб, итоговый винрейт: -2 бб /100. Игра по GTO в 3-max отнимает у нас деньги из-за появления фиша, играющего не по GTO!
А если на большом блайнде находится сильный игрок, способный на эффективные подстройки, ситуация становится для нас еще хуже! Отклонение ББ от равновесия Нэша больше не ведет к понижению его собственного EV – это условие работает только тогда, когда все трое играют по GTO. Заметив изменение стратегии баттона, большой блайнд может подстроиться, еще сильнее снижая... наш винрейт! Если ББ сузит свой диапазон оверколла, мы на малом блайнде дополнительно потеряем почти 1 бб / 100!
Наша модель считается в фишках, т. е. применима для кэш-игры. В МТТ или SNG, где расчеты проводятся по ICM, «фактор фиша» зачастую становится еще более значимым, делая игру по Нэшу еще менее выгодной.
Вывод
Мы не пытаемся осуждать игру по GTO. Стратегия GTO непобедима для любых ситуаций с участием двух игроков, и даже для мультипотов понимание теории покера позволит вам эффективнее балансировать диапазоны и улучшать свое ожидание. Я верю, что развитие стратегий GTO будет основной движущей силой в покере в следующие пять лет. Однако считайте этот текст предостережением для тех, кто готовится отключить свой мозг и слепо играть по GTO в любой ситуации. Тот, кто ошибочно опирается на теорию в ситуациях, где она неприменима, использует ее как костыль, а не как инструмент, и неизбежно отстанет от своих соперников.

































Soul решил попереть против нобелевского лауреата, который доказал существование равновесия для всех конечных игр ещё в 1950м году.
2011 год :)
Года через 2, если кто-то сыграл на нл25 не по ГТО его будут обсуждать и смеяться над ним на всех покерных форумах, и очереди за ним будут из тысяч регов.
И феруэл уже так и не выпустит из рук дробовика.
даёшь покерные стримы в массы!!!
Равновесие сработало. Если ответ на твой комментарий собирает n плюсов, то сам комментарий соберет n минусов.
Не совсем ясно, с какой целью нам бы потребовалось играть идеально по ГТО против рыбы, допускающей много ошибок.
Но не исключено, что вы слышали про такую форму покера, которая называется "кэш-игра"...